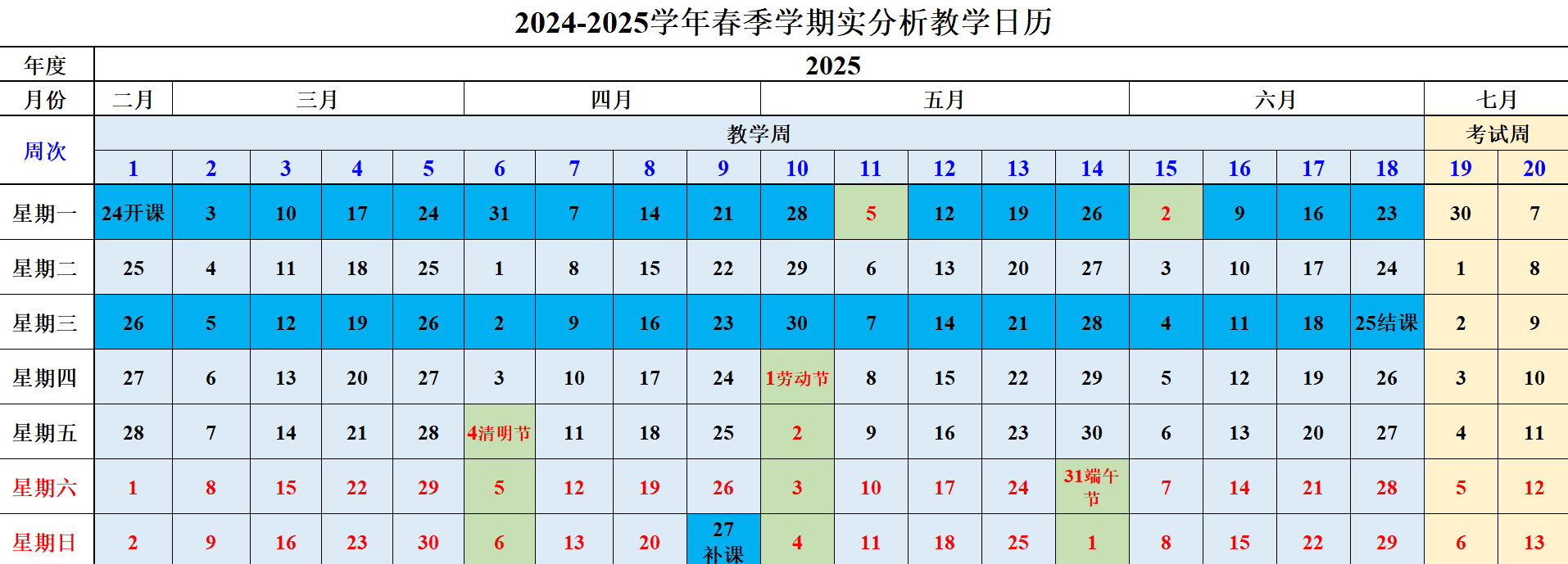
\( \def\<#1>{\left<#1\right>} \newcommand{\CC}{\mathcal{C}} \newcommand{\eps}{\varepsilon} \newcommand{\ls}{\leqslant} \newcommand{\gs}{\geqslant} \newcommand{\norm}[1]{\|#1\|} \usepackage{resmes} \newcommand{\mres}{\resmes} \usepackage{cases} \newcommand{\dv}{\mathrm{div}} \newcommand{\R}{\mathbb{R}} \newcommand{\D}{\partial} \)
实分析 2025春季学期

2025春季：实分析


授课教师 郝成春（邮箱地址: hcc[at]amss.ac.cn，办公室：中科院数学院南楼915）
上课地点 中国科学院大学玉泉路校区 教学楼阶二2
上课时间 星期一、三（第1-2节） 8:00-9:40
习题课 助教: 付杰, 电子邮箱: fujie[at]amss.ac.cn， 周三(第9-10节: 6:10~7:50pm) 教学楼305
相关通知
  • 2月24日：开课（星期一）。
  • 3月12日的习题课调到该周六（3月15日）1:30-3:10pm， 教室305。
  • 清明节：4月4-6日放假。
  • 劳动节：5月1-5日放假调课，4月27日（周日）补5月5日（周一）的课。
  • 期中考试时间：5月7日（周三）8:00-9:40，随堂考，地点：阶二2。
  • 端午节：5月31日至6月2日放假停课。
  • 6月25日：最后一次课（星期三）。
  • 期末考试：6月30日（周一）上午09:00-11:00，阶一4
教材
  1. Stein & Shakarchi, Real Analysis: Measure Theory, Integration, and Hilbert Spaces, 影印版, 世界图书出版公司, 2013. (ISBN：978-7-5100-4053-5) 引言, 第 1–3, 6 章. [$\gg$非官方勘误表]、[$\gg$官方勘误表]
  2. Folland, Real Analysis：Modern Techniques and Their Applications, 第 2 版影印版, 世界图书出版公司, 2019. (ISBN：978-7-5192-6072-9) 第 0,3,6 章. [$\gg$官方勘误表]
  3. Royden & Fitzpatrick, Real Analysis, 第 4 版影印版, 机械工业出版社, 2020. (ISBN: 978-7-111-64665-5) 第 16 章. [$\gg$勘误表]

周次日期及课堂内容作业
124/2: [SS,F]引言；集合的运算及势
26/2: 有序集、度量空间		 已过期，不再显示下载链接。
2 3/3: 度量空间（续）
5/3: $\sigma$-代数、开集的构造、Cantor三分集		已过期，不再显示下载链接。
3 10/3: [SS]第1章, 外测度及性质、Lebesgue测度
12/3: 可测集、可测集逼近定理、内正则性、Vitali的不可测集构造		已过期，不再显示下载链接。
4 17/3: 可测函数的定义、性质、简单函数逼近
19/3: 阶梯函数逼近、Egorov定理		已过期，不再显示下载链接。
5 24/3: 依测度收敛、Riesz定理、Lusin定理
26/3: [SS]第2章，Lebesgue积分的基本性质		已过期，不再显示下载链接。
6 31/3: 有界收敛定理、Lebesgue积分与Riemann积分的关系，Fatou引理、单调收敛定理
2/4: 积分的绝对连续性、Lebesgue控制收敛定理, 可积函数空间$L^1$		已过期，不再显示下载链接。
7 7/4: $L^1$的完备性、$L^1$中稠密函数类、积分的不变性、平移与连续性
9/4: Fubini定理、Tonelli定理及其推论 		已过期，不再显示下载链接。
8 14/4: Fubini定理的应用；
16/4: [SS]第3章：积分的微分，Hardy-Littlewood极大函数定理、Lebesgue微分定理、Lebesgue集 		已过期，不再显示下载链接。
9 21/4: 好核、恒等逼近、
23/4: 有界变差函数、Jordan分解定理、
27/4: (补课)旭日引理、函数的可微性、 		已过期，不再显示下载链接。
10 28/4: 绝对连续函数、Vitali覆盖定理II、
30/4: Lebesgue积分的微积分基本定理、跳跃函数		已过期，不再显示下载链接。
11 5/5: 劳动节放假, 调至4月27日
7/5: 期中考试		本周无作业
12 12/5: 跳跃函数（续）、可求长曲线、
14/5: [SS]第6章，抽象测度、 Carathéodory定理、度量外测度 		已过期，不再显示下载链接。
13 19/5: 度量外测度（续）、准测度
21/5: Carathéodory-Hahn延拓定理、可测函数、积分定义和性质、乘积测度、		已过期，不再显示下载链接。
14 26/5: 一般的Fubini定理、
28/5: 极坐标积分公式、$\Bbb{R}$上的Borel测度与Lebesgue-Stieltjes积分、 		已过期，不再显示下载链接。
15 2/6: 端午节假期停课
4/6: 带号测度、Jordan分解定理、		本周无作业，复习
16 9/6: Lebesgue-Radon-Nikodym定理、
11/6: 复测度与Lebesgue-Radon-Nikodym定理、 [F]第6章，$L^p$空间，		已过期，不再显示下载链接。
17 16/6: Hölder不等式、Minkowski不等式、$L^p$完备性、稠密性、$L^\infty$、
18/6: 空间嵌入关系、$L^{p'}$范数的对偶表示、		已过期，不再显示下载链接。
18 23/6: Riesz表示定理、
25/6: [RF]第16章，内积、正交性、		本周无作业

  2025-07-12   上午好！ |   © 2007-2025 C. C. Hao